The Millionaire Problem: Who’s Got More Cash?

Imagine you’re at a fancy party with two millionaires, Alice and Bob. They want to know who’s richer but without spilling the beans about their actual fortunes. This puzzle, known as the Millionaire Problem, is a classic brain-teaser in the world of cryptography, dreamt up by Andrew Yao back in 1982.

The Basic Idea

  • Goal: Alice and Bob want to find out who’s wealthier without revealing their exact net worths to each other.
  • Scenario: Alice has a net worth of ( A ) and Bob has ( B ). They need to figure out if ( A > B ) or ( B > A ) without either of them knowing the actual amounts.

The Cryptographic Magic

To solve this, there are a few cryptographic tricks up our sleeves:

  1. Yao’s Garbled Circuits: Think of this as a magic box where they can input their encrypted numbers and get an answer about who’s richer without revealing the numbers themselves. It’s one of the earliest and coolest solutions to this problem.

  2. Homomorphic Encryption: This is like doing math on encrypted data. Alice and Bob can compare their wealth without decrypting it, so they get the answer but keep their fortunes secret.

  3. Oblivious Transfer: Here, one can send a secret piece of information without knowing what’s been sent. It’s another neat way to keep their numbers under wraps while still figuring out who’s got more money.

Real-World Uses

This problem isn’t just for fun; it’s super useful in real life:

  • Privacy-Preserving Data Mining: Companies can analyze shared data without exposing private details.
  • Secure Auctions: Bidders can participate without revealing their bids until the winner is declared.
  • Financial Privacy: It ensures secure and private financial transactions, like in zero-knowledge proofs.

How It Works (Simplified)

  1. Agree on the Method: Alice and Bob decide on a secure way to encrypt their numbers.
  2. Encrypt the Numbers: Both encrypt their wealth.
  3. Compare Securely: They use the agreed method to compare the encrypted values without decrypting them.
  4. Get the Result: They find out who’s richer without knowing the exact amounts.

Here the serious references

Check out these sources to geek out on the technical details:

  • Andrew Yao’s Original Paper: IEEE Xplore
  • Foundations of Cryptography by Oded Goldreich
  • Introduction to Modern Cryptography by Jonathan Katz and Yehuda Lindell

Is it crystal clear now? Not for me.

Let’s see an example for kids

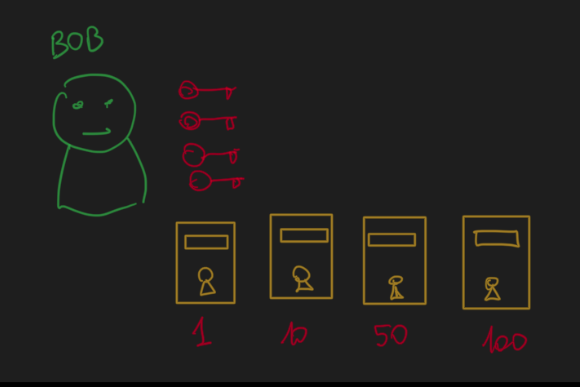
Bob builds 4 boxes with 4 keys

Every box has a label with the “wealth” in millions (of candies)

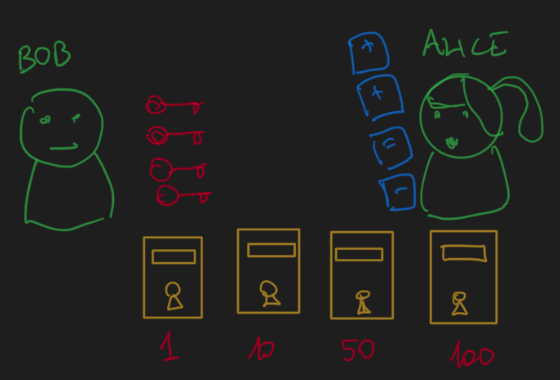
Alice writes 4 notes with symbols + - =

and slips one inside each box

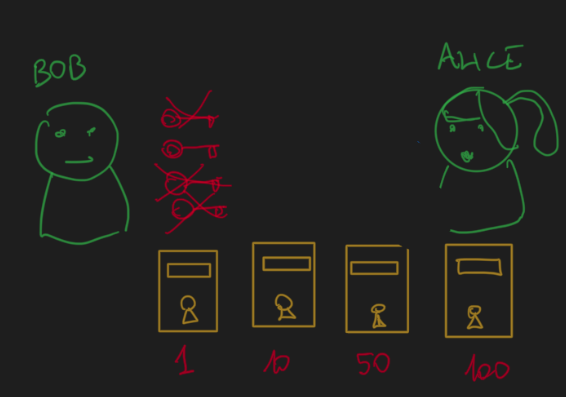
Bob destroys all the keys except the one with “his” wealth box.

Alice can verify Bob has destroyed the other keys but she does not know which key is kept by Bob

Alice leaves the room and Bob can only open the box with “his” wealth

…. and he can discover that Alice has:

  • more candies (+)
  • more or less the same (=)
  • less candies ( - )

than himself